Class 10 BPT Basic Proportionality Theorem

 Statement: 

BPT (Basic Proportionality Theorem), 

If a line is drawn parallel to one of the  triangle to intersects the other two sides in distinct points, 

then the other two sides of 

the  triangle are divided  into the same ratio. 

Proof:

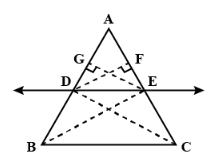
Given:

In ∆ABC, DE || BC and AB and AC are intersected by DE at points D and E respectively.

To prove:

AD / DB = AE / EC

Construction:

Join BE and CD.and

Draw:

EG⊥AB and DF⊥AC

Proof:

We know that

ar( Δ ADE) = 1 / 2 × AD × EG   

ar( Δ DBE) = 1 / 2 × DB × EG   

So

ar(Δ ADE) / ar(Δ DBE) =

 AD / DB   ------- (1)

Similarly,

ar(Δ ADE) / ar(Δ ECD) =

 AE / EC   ----------(2)

Now, 

Δ DBE and Δ ECD

are the on the same base DE and also between the same parallels i.e. DE and BC,

So

ar(Δ DBE) = ar(Δ ECD)  ---(3)

By (1), (2) , (3) 

AD / DB = AE / EC  

Hence  proved.