Area of similar triangle

OBJECTIVE

To verify that the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides. 

PREREQUISITE KNOWLEDGE

Concept of parallel lines

MATERIALS REQUIRED

Scissors

Geometry box

Colours

White paper

PROCEDURE

Take a white chart paper and cut a ∆ABC with 

AB=6cm,  

 BC=6cm, 

 CA=6cm

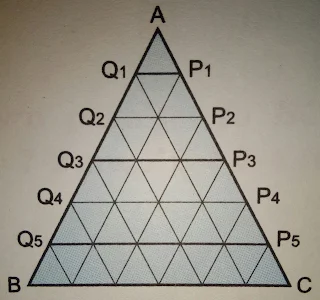
Mark five points P1,P2,P3,P4,P5 at a distance of 1 cm on side AC and

Q1,Q2,Q3,Q4,Q5 at a distance of 1 cm on side AB. ( Image 1)

                                                                          Image 1

Join P1Q1,P2Q2,....P5Q5  

Draw parallel line to  AC from Q1, Q2....

and parallel line to AB from P1, P2,.( Image 2)

                                                                           Image 2

This ∆ ABC is divided into 36 similar and equal in area of triangles.

Construct a  ∆ PQR 

with PQ= Half of AB

        PR=Half of AC  

        QR=Half of BC on other chart paper

Mark D1,D2  and E1,E2 on sides PQ and PR ( Image3)

                                                                            Image 3

Divide  ∆ PQR into 9  similar and equal in areas triangles ( Image 4)

                                                                           Image 4

OBSERVATION

Area of   ∆ABC=Area of 36 smaller triangles

Area of  ∆ PQR=Area of 9 smaller triangles

CONCLUSION

It is Verified that the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides.