Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
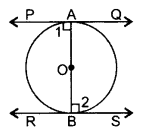
∠1 = 90° …(i)
∠2 = 90° …(ii)
∠1 = ∠2----by (1) &(2) (AIA)
∴PQ || RS
Let AP and BP be the two tangents drawn from external point P to the circle with centre O.

To Prove : AP = BP
Proof :
In Δ AOP and Δ BOP
OA = OB (radii)
∠OAP=∠OBP=90∘
(Line drawn from from center to the tangent through the point of contact is perpendicular)
OP = OP (common)
∴ΔAOP≅ ΔBOP (R.H.S.)
∴ AP = BP ( C P C T )
Therefore the length of the
tangents drawn from an
external point to a circle are
equal.
Q 3. Statement:
BPT (Basic Proportionality Theorem),
If a line is drawn parallel to one of the triangle to intersects the other two sides in distinct points,
then the other two sides of
the triangle are divided into the same ratio.
Proof:
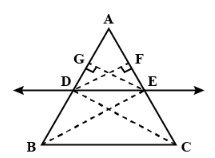
Given:
In ∆ABC, DE || BC and AB and AC are intersected by DE at points D and E respectively.
To prove:
AD / DB = AE / EC
Construction:
Join BE and CD.and
Draw:
EG⊥AB and DF⊥AC
Proof:
We know that
ar( Δ ADE) = 1 / 2 × AD × EG
ar( Δ DBE) = 1 / 2 × DB × EG
So
ar(Δ ADE) / ar(Δ DBE) =
AD / DB ------- (1)
Similarly,
ar(Δ ADE) / ar(Δ ECD) =
AE / EC ----------(2)
Now,
Δ DBE and Δ ECD
are the on the same base DE and also between the same parallels i.e. DE and BC,
So
ar(Δ DBE) = ar(Δ ECD) ---(3)
By (1), (2) , (3)
AD / DB = AE / EC
Hence proved.
Q 4.
Prove √3 is a Irrational number.
Proof:
Let √3 be a rational number.
So, √ 3=p ____ (1) q
On squaring both sides
3=p2q2
q2= p23
⇒3 is a factor of p2
⇒3 is a factor of p.
Now, again let p = 3 c.
So, √ 3= 3 cq
On squaring both sides
3= 9 c2q2
q2=3 c2
c2= q23
⇒3 is factor of q2
⇒3 is a factor of q.
Here 3 is a common factor of p, q both
So p, q are not co-prime.
Therefore our assumption is wrong.
√3 is an irrational number.
Q 5.
Let AP and BP be the two tangents drawn from external point P to the circle with centre O.
To Prove : AP = BP
Proof :
In Δ AOP and Δ BOP
OA = OB (radii)
∠OAP=∠OBP=90∘
(Line drawn from from center to the tangent through the point of contact is perpendicular)
OP = OP (common)
∴ΔAOP≅ ΔBOP (R.H.S.)
∴ AP = BP ( C P C T )
Therefore the length of the
tangents drawn from an
external point to a circle are
equal.
Q 3. Statement:
BPT (Basic Proportionality Theorem),
If a line is drawn parallel to one of the triangle to intersects the other two sides in distinct points,
then the other two sides of
the triangle are divided into the same ratio.
Proof:

Given:
In ∆ABC, DE || BC and AB and AC are intersected by DE at points D and E respectively.
To prove:
AD / DB = AE / EC
Construction:
Join BE and CD.and
Draw:
EG⊥AB and DF⊥AC
Proof:
We know that
ar( Δ ADE) = 1 / 2 × AD × EG
ar( Δ DBE) = 1 / 2 × DB × EG
So
ar(Δ ADE) / ar(Δ DBE) =
AD / DB ------- (1)
Similarly,
ar(Δ ADE) / ar(Δ ECD) =
AE / EC ----------(2)
Now,
Δ DBE and Δ ECD
are the on the same base DE and also between the same parallels i.e. DE and BC,
So
ar(Δ DBE) = ar(Δ ECD) ---(3)
By (1), (2) , (3)
AD / DB = AE / EC
Hence proved.
Q 4.
Prove √3 is a Irrational number.
Proof:
Let √3 be a rational number.
So, √ 3=p ____ (1) q
3=p2q2
q2= p23
⇒3 is a factor of p2
Now, again let p = 3 c.
So, √ 3= 3 cq
3= 9 c2q2
q2=3 c2
c2= q23
⇒3 is factor of q2
⇒3 is a factor of q.
Prove that the parallelogram circumscribing a circle is a rhombus.
ABCD is a parallelogram , So opposite sides of a parallelogram are equal.
AB=CD.
BC=AD.-----++++(1)
DR=DS --------------(2)
(Tangents on the circle from same point D)
Similarly
CR=CQ ----------(3)
AP = AS ------------(4)
PB = BQ -------++(5)
Adding all these equations we get
DR+CR+BP+AP=DS+CQ+BQ+AS
(DR+CR)+(BP+AP)=(DS+AS) +( BQ + CQ)
CD+AB=AD+BC
But AB =CD & BC=AD
AB + AB = BC + BC
2AB=2BC
Therefore AB=BC -------(6)
From equation (1), & (6) we get
AB=BC=CD=DA
∴ABCD is a Rhombus
Q 6. Find relationship between x and y such that the point P(x, y) is equidistant from the points A (2, 5) and B (-3, 7)
Solution:
Let P (x, y) be equidistant from the points A (2, 5) and B (-3, 7). so
∴ AP = BP
AP 2 = BP 2
(x – 2)2 + (y – 5)2 = (x + 3)2 + (y – 7)2
x2 – 4x + 4 + y2 – 10y + 25 =x2 + 6x + 9 + y2 – 14y + 49
⇒ -4x – 10y +29 = 6x - 14y +58
⇒ -10x + 4y = 29
is the required relation.
Q 6.
Find relationship between x and y such that the point P(x, y) is equidistant from the points A (2, 5) and B (-3, 7). (2011D)
Solution:
Let P (x, y) be equidistant from the points A (2, 5) and B (-3, 7). so
∴ AP = BP
AP 2 = BP 2
(x – 2)2 + (y – 5)2 = (x + 3)2 + (y – 7)2
x2 – 4x + 4 + y2 – 10y + 25 =x2 + 6x + 9 + y2 – 14y + 49
⇒ -4x – 10y +29 = 6x - 14y +58
⇒ -10x + 4y = 29
is the required relation.
Q7. Draw the graph of 2x + y = 6 and 2x – y + 2 = 0. Shade the region bounded by these lines and x-axis. Find the area of the shaded region. [CBSE 2007]
Solution:
The given system of equation is
2x + y – 6 = 0 ………. (i)
2x – y + 2 = 0 ……… (ii)
solutions for each equation of the system are:
(i) ⇒ y = 6 – 2x
Table of solutions for 2x + y – 6 = 0

Similarly
Table of solutions for 2x – y + 2 = 0

Plotting these on the graph
These intersect at (1, 4), so this is the solution.
In graph, area bounded by the lines and x-axis is
∆PAB which is shaded.
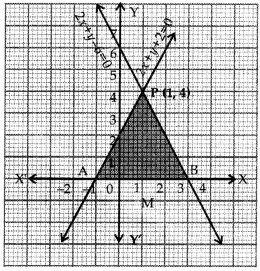
Draw PM ⊥ x-axis
PM = y-coordinate of P (1, 4) = 4 units
and AB = 1 + 3 = 4 units
∴ Area of shaded region
= Area of ∆PAB = 12 × AB × PM
= 12 × 4 × 4 = 8 sq. units.
Let P (x, y) be equidistant from the points A (2, 5) and B (-3, 7). so
∴ AP = BP
AP 2 = BP 2
(x – 2)2 + (y – 5)2 = (x + 3)2 + (y – 7)2
x2 – 4x + 4 + y2 – 10y + 25
⇒ -4x – 10y +29 = 6x - 14y +58
⇒ -10x + 4y = 29
is the required relation.
Find relationship between x and y such that the point P(x, y) is equidistant from the points A (2, 5) and B (-3, 7). (2011D)
Solution:Let P (x, y) be equidistant from the points A (2, 5) and B (-3, 7). so
∴ AP = BP
AP 2 = BP 2
(x – 2)2 + (y – 5)2 = (x + 3)2 + (y – 7)2
x2 – 4x + 4 + y2 – 10y + 25
⇒ -4x – 10y +29 = 6x - 14y +58
⇒ -10x + 4y = 29
is the required relation.
Draw the graph of 2x + y = 6 and 2x – y + 2 = 0. Shade the region bounded by these lines and x-axis. Find the area of the shaded region. [CBSE 2007]
Solution:
The given system of equation is
2x + y – 6 = 0 ………. (i)
2x – y + 2 = 0 ……… (ii)
solutions for each equation of the system are:
(i) ⇒ y = 6 – 2x
Table of solutions for 2x + y – 6 = 0
Similarly
Table of solutions for 2x – y + 2 = 0
Plotting these on the graph
These intersect at (1, 4), so this is the solution.
In graph, area bounded by the lines and x-axis is
∆PAB which is shaded.

Draw PM ⊥ x-axis
PM = y-coordinate of P (1, 4) = 4 units
and AB = 1 + 3 = 4 units
∴ Area of shaded region
= Area of ∆PAB =
=




